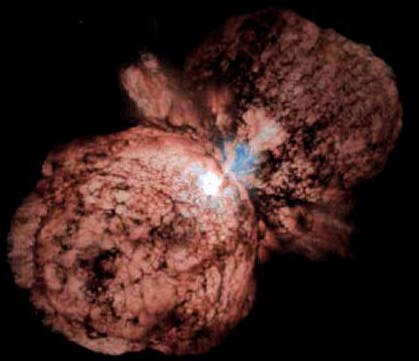
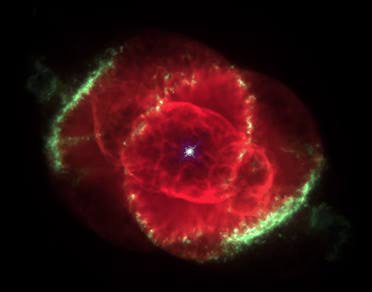
I love this star! I described to my wife Beth -- before I saw this star or any other similar planetary nebula -- that stars should, according to the Ball-of-Light Particle Model explode with this geometry. When I first saw a photo of this star, I was simply in awe! Here, in one very graphic image, was a summary of the Ball-of-Light Particle Model. This star is a perfect example of the Ball-of-Light Particle Model.
Look at this image carefully. The most important aspect is the shape of the two spherical lobes is formed by electric, magnetic and gravitational fields. Note the longitude and latitude "lines" in the spherical lobes due to the electric and magnetic fields. For those of you familiar with Spherical Harmonics, this is a spherical harmonic.
Let me first address this key issue, if stars are collapsed clouds of gas and dust -- as current astrophysical theory explains -- then current astrophysical theory can not explain how a star could eject material in this fashion.
I have created an animated GIF to demonstrate, in a very rough way, how this star is exploding. (I have another animation, an animated GIF of a photon, which is very similar to this animation. There is a good reason they are similar. The same equation -- E cross B = G -- describes both situations.)
Traditional astrophysics can not explain why the two lobes are curving back around -- and where the "lines" in the nebula are coming from. If the core of a star is a ball-of-light, and acts as the Ball-of-Light Particle Model predicts, then it is easy to explain how a star explodes like this.
Before continuing, it should be noted, Eta Carinae is not a fluke. There have been many other images taken from the Hubble Space Telescope and from other telescopes of planetary nebulae with the same, or similar, geometry as Eta Carinae. A few examples include:

(Some of these images are from http://www.ozemail.com.au/~mhorn/img_pneb)
In the bottom right image -- that of NGC6302 -- note how the lobes have not completely turned yet. They have started to turn or "curve back", on the way to becoming spherical, but are only about halfway formed.
(Some scientists refer to this geometry of planetary nebula as "butterfly" shaped. I prefer to think of these shapes in terms of spherical harmonics. Some of these nebula have also been referred to as "dumbbell" shaped. While this better describes the three dimensional shapes of the nebula, it would still be better to use spherical harmonics. The disk in Eta Carinae's structure would be hard to describe in the context of "butterfly" shaped, or "dumbbell" shaped, but there is a spherical harmonic for this shape.)
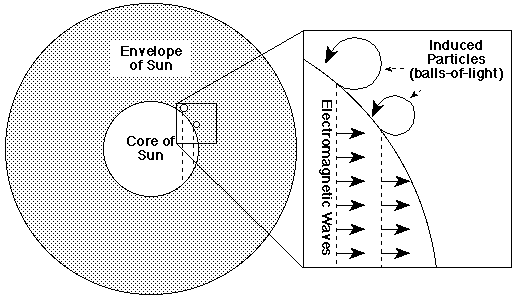
To understand Eta Carinae it is important to understand what the Ball-of-Light Particle Model predicts a star is, and how they form. The Ball-of-Light Particle Model predicts the core of a star is a single ball-of-light. In a normal star, this central core is surrounded by an envelope of plasma made up of electrons and normal atomic nuclei such as protons. An example of this can be seen in the following graphic of our sun's core surrounded by its outer envelope of plasma.
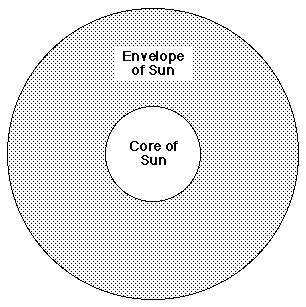
A critical question is, Where does the material
in the envelope of a star come from?
Traditional astronomical theory predicts preexisting gas and dust collapse gravitationally to form a star. The Ball-of-Light Particle Model predicts the core of stars make, or more precisely, electromagnetically induce the particles of gas and dust that are often found around stars. In other words, the central core comes first, making the surrounding plasma and surrounding clouds of gas and dust.
To summarize, the source of the material in the enveloping plasma around the core of a star is -- contrary to traditional stellar theory -- the central core. (See also, The Induction of Matter, Induction off of the Sun's Core)
Since this is such an important deviation from traditional theory, I will state it again with different wording. The central core's electromagnetic fields induce new particles at the surface of the core. According to the Ball-of-Light Particle Model, stars are not plasma all of the way to their centers. According to the Ball-of-Light Particle Model, stars are not collapsed clouds of gas and dust. Stars are decaying balls-of-light.
The Ball-of-Light Particle Model can be visualized by the following graphic.
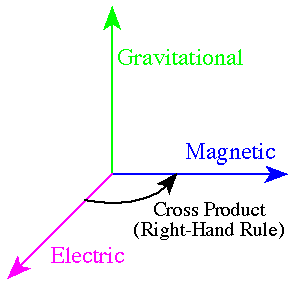
When analyzed over a spherical wave, the wave's fields could be resented as in the following graphic.
The central pointing green arrows in this animation of a moving photon represent the gravitational field. The electric, magnetic, and gravitational fields pivot around each other -- each inducing the other in a perfectly symmetrical fashion -- allowing the photon to propagate billions of light-years through space without dissipating. In almost exactly the same fashion, the electromagnetic waves on the core of Eta Carinae are sweeping off the core. They induce a strong central pointing gravitational field turns the nebula, curving the lobes around in a spherical pattern.
As an example, imagine an otherwise normal star. Its core develops two massive electromagnetic waves that start sweeping across the core from the equator towards the poles. (An example of what might start these waves is a very large planet, comet, or star that spirals in around the star.)
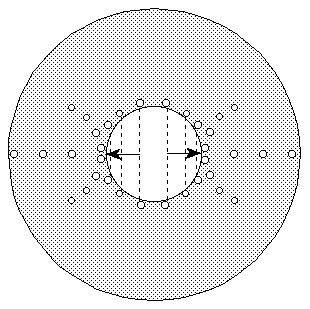
In this figure the dashed lines on the core are the first key item. They represent the waves on the core of the star. Each wave is like a ring around the star. Each wave intensifies as it approaches the poles. Induced particles will sweep off the ends of the poles of the core following specific patterns that are a direct result of the electromagnetic fields on the core of the star. Some balls-of-light are ejected straight off the poles of the core, some are ejected in hemispherical patterns. The balls-of-light that are ejected straight off the poles would be more massive and would have trajectories determined by their inertia. The balls-of-light that are ejected hemispherically would be less massive and their trajectories would be determined by the electromagnetic fields from the core of the star.
Not only does the core of the star have intense electromagnetic fields, the induced balls-of-light have powerful electromagnetic fields of their own. They can not just pass through the enveloping plasma that surrounds the core without having some effect on the ions in the plasma. In essence, the ejected balls-of-light will sweep some, or all, of the plasma off the core. As material is swept off the core, the outer plasma of the star will start to take on an unusual shape -- as depicted in the next figure.
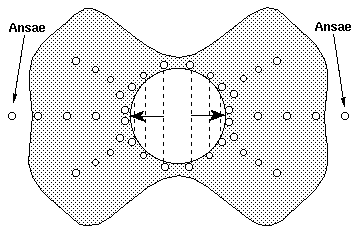
What happens to the smaller balls-of-light will depend on how harmonic they are. Some of the more harmonic ejected balls-of-light can shoot out of the plasma. Those ejected straight off the poles will become what are known as Ansae.
Some of the less harmonic ejected balls-of-light may explosively decay before they escape the lobes of the nebula. Examples of ejected balls-of-light decaying explosively like this can be seen in the image of M2-9 above -- labeled "C".)
Most of the ejected balls-of-light will probably decay rather rapidly into normal elementary particles and not make it very far from the star.
(Note, upon decay, larger balls-of-light give off characteristic nonthermal radiation in powerful burst of x-ray and gamma-ray radiation. Powerful x-ray bursts from decaying balls-of-light in the Corona of our sun can be viewed at any time by going to the website for Current Solar Data. At this site, see also, X-Ray Image of Sun -- Showing Decaying balls-of-light.)
When a wave reaches a pole, some of its energy will be lost in the form of photons and ejected balls-of-light. However, much of the wave's energy will rebound and travel in the opposite direction. As the waves continue to sweep back and forth over the core, more balls-of-light are ejected, and more of the outer plasma envelope of the star is stripped away. This back and forth sweeping of the electromagnetic waves will create recurring patterns in the radiation output from planetary nebulae like Eta Carinae. This process will continue to shape the outer plasma of the star -- as depicted in the following diagram.
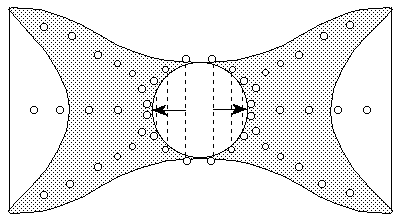
Eventually, in this spherical harmonic pattern -- caused by two oppositely directed massive waves -- the nebula forms into the double-lobed shape -- a spherical harmonic.
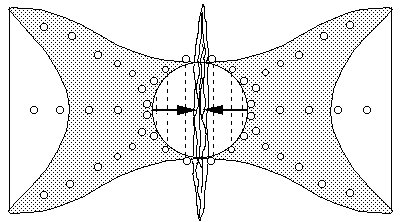
When the two primary waves change direction and collide at the equator of the core, they will induce an equatorial wave that ejects material off the equator of the core. If the two primary waves were originally induced by a large body spiraling around the star, then this wave will continue to have a spiraling component.
If the spiraling body that starts the primary waves has a coil trajectory rather than a planar trajectory as is shown in the next figure,
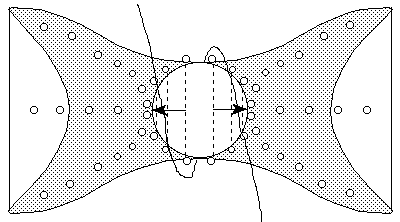
then, it will develop spiraling ansae-like streams of decaying balls-of-light like in the Cat's Eye Nebulae.
(The above graphics did not turn out exactly as I would like. I will upload a better representation when I have the time.)
The example of Eta Carinae and the earlier examples of planetary nebulae have just one lobe off each end the star. If the central core has enough energy, it should be possible to see the pattern repeat and have more than one wave. In essence, more than one spherical wave, or "lobe" will be observed lined up off the ends of some stars -- or cores of galaxies. I believe this is exactly the pattern seen in many Radio Galaxies.
The size of the induced particles in the enveloping plasma of stars are a function of the intensity of the electromagnetic waves on the core's surface. If a wave is too weak, it does not induce a particle -- maybe just a photon. If it is intense enough, it induces a small particle. For normal stars, a "small" particle would be "normal" elementary particles such as electrons or protons. If the electromagnetic wave is very intense, it will induce a large particle. For normal stars, a "large" particle might be tens, hundreds or possibly thousands of kilometers in diameter. (See also, Blinkers, Sunspots, and Radio Galaxies for examples of ridiculously large induced balls-of-light.)
The Ball-of-Light Particle Model predicts the core of a star is an extremely large ball-of-light that has been induced, in like fashion, off the core of a galaxy.
After the waves have swept the outer plasma off the core of a star, then what is left?
The core of the star, the central ball-of-light, a white dwarf.
In many instances, very harmonic stars have no outer envelope of plasma -- or very little plasma. These stars have been named white dwarfs. White dwarfs have also been found in the centers of novas, supernovas, and planetary nebula. One of the hottest stars ever discovered is the bared core of the planetary nebula NGC 2440. Its temperature has been estimated to be 200,000 degrees Kelvin -- compared to the sun's temperature of 6,000 degrees Kelvin!
This temperature is just an estimate though. Scientists estimate the temperature of stars by analyzing the star's light. Normally, the outer plasma envelope of a star gives off light in the form of thermal radiation. In contrast, the light induced off the surface of a ball-of-light by the electromagnetic waves is in the form of nonthermal radiation. Thus scientists have difficulty estimating the temperatures of the stars at the center of planetary nebula because they are nonthermal sources of radiation, not thermal. Of course, this is an observational fact that supports the Ball-of-Light Particle Model.
How are the waves arranged on the surface of a star's core? For a harmonic core, the waves are evenly spaced and small. For a nonharmonic core, the waves are not evenly spaced and can become large.
(This image is not exactly what I would like. Instead of patches of electric and magnetic fields arranged in this manner, all of the patches would have the same size and geometry -- or at least, each would be smaller size and have the same surface area. However, this image does nicely represent the idea of having alternating patches of electric and magnetic fields.)
A nonharmonic core would have patches of electric and magnetic fields that were larger than the majority of others. Furthermore, they would likely be arranged in unusual, or unequally spaced patterns.
(Again, this image did not turn out exactly as I wished. I will upload a better graphic when I have the time. I would have preferred the alternating patches of electric and magnetic fields to be equal in area and much smaller in size.)
The non harmonic patches on the core of a star like our sun could induce large balls-of-light that would float up through the envelope and be visible. We call them sunspots.
A large animated GIF (161K) of a ball-of-light inducing a smaller ball-of-light off of its pole here.
With some patterns, the waves could gradually dissipate and the star would become more stable. With other patterns, the decay mode could be self-inducing and the waves would accelerate until the star explodes in a Supernova.
If one large instability formed on the core it could spiral around the core while inducing a stream of particles. This has been observed in a Wolf-Rayet star observed by the Keck telescope.
This star is called Wolf-Rayet WR 104.
During the lifetime of the majority of stars in the universe, the waves on the core of the star would be harmonic. The stellar core would slowly decay. The majority of the induced atomic nuclei would be small -- i.e., "normal" elementary particles such as electrons and protons. The core would simply "fizzle" out.
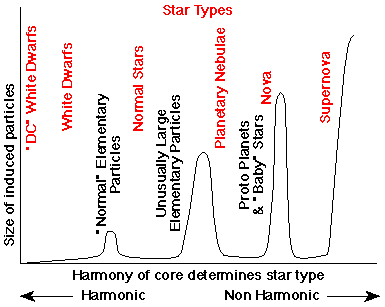
This graph illustrates how, as the core of a star is more harmonic, it decays slower, giving off just photons or small particles, and how as it is less harmonic, it decays faster, giving off larger and larger balls-of-light. This process does not happen in a continuous fashion however. Due to the harmonics, a mostly harmonic star will induce the relatively small "normal" elementary particles. This hump in the graph would include all elements in the periodic table of elements. A normal star -- like our sun -- can induce elementary particles with much larger proportions though. (See also Sunspots and Blinkers.) As a star becomes less harmonic, it may go into a phase where it becomes a planetary nebulae, where it ejects larger balls-of-light. In the Nova harmonic the core may frequently induce larger balls-of-light that are called "baby" stars -- that may slowly fizzle out and cool to form planets. In nova, or supernova the star may simply break apart into large chunks or explosively decay into photons and small balls-of-light.
A star that is almost perfectly harmonic will have electromagnetic fields on the surface of its core that only induce photons. These photons will not be slowed by the envelope of plasma that surrounds most normal stars. Thus these stars will seem extremely hot when measured with normal spectroscopy. Also, with no envelope of plasma, the photons emitted by the core will take on a continuum with spectral lines -- "nonthermal" radiation. This type of star is called a "DC" White Dwarf. Thus, the Ball-of-Light Particle Model predicts White Dwarfs are the exposed core of a star -- an exposed ball-of-light. Some White Dwarfs have spectral lines because they are closer to the first hump in the graph above -- that is, they have a thin outer envelope of "normal" elementary particles that absorb the radiation from the core and then re-emit the radiation with characteristic spectral lines. As the outer envelope of plasma gets thick enough, the star appears cooler and takes on the appearance of a normal star.
For some stars, the core might develop an unusual harmonic with very strong, larger electromagnetic waves. These stronger waves could induce larger particles. For example, there is a type of star that has been observed that has an unusually high amount of an atomic nuclei called, "technetium" in its enveloping plasma. Technetium has a very heavy atomic nucleus. This type of material should not be found on the surface of stars according to the classical theory of star formation. According to traditional theory, these heavy atomic nuclei should "sink" to the bottom of the plasma -- to the center of the star. The classical theory for star formation can not explain the abundance of this material on the surface of these stars.
How the star gets the heavy elements from the core to the surface without exploding provides an impressive challenge to theoreticians. 40 (L. H. Aller)
Only nuclear reactions in the surface layers of the stars can account for the presence of technetium lines in type S stellar spectra. 41 (Shklovsky)
If technetium or other heavy elements are manufactured in the core of stars, then the traditional theory of star formation can not explain why this heavy material floats to the surface of these stars. Furthermore, if stars can get technetium or other heavy elements only from supernova, then current theory can not explain how this material becomes concentrated in individual stars and, again, floats on the surface of the plasma.
The Ball-of-Light Particle Model predicts that the cores of stars such as this have intense electromagnetic waves -- intense enough to produce copious amounts of heavy metal atomic nuclei. Its just that these harmonics are rare, and perhaps are even transitory, thus the stars are rare. However, there is no difficulty explaining heavy metals on the surface of a star's plasma envelope. In such stars the entire envelope would have a high percentage of heavy atomic nuclei -- the sizes being a function of the harmonic waves on the core of the star.
Thus, the Ball-of-Light Particle Model predicts Eta Carinae could have heavy elements.
Some of the waves on the core of stars are slow but large. They are not intense enough to induce individual particles, but they are strong enough to induce the plasma to move in the form of waves in the outer envelope. Such a wave, or a pair of waves, that circle the entire circumference of the star's core could help create a nebula like Eta Carinae's.
At the other extreme some waves are unbelievably powerful. The wave that sweeps across a Pulsar is just such and example.
Imagine the situation where a star's core that has just one massive wave sweeping back and forth from pole to pole.
A single massive wave might be started by a large object impacting the surface of the star. The impact point would define a new "pole" for the star. The wave would sweep around the star. As it sweeps past the new "equator" of the star the strength of the wave would be weakest. As the wave sweeps around the opposite side of the star, the strength of the wave would become increasingly more intense until it converges at the pole on the opposite side of the impact.
What happens to the plasma in the outer envelope of the star as this wave converges?
What happens to the wave after it reaches the pole on the opposite side of the impact?
As the wave focuses its energy at the pole on the side opposite of the impact, some of the plasma of the star would be ejected. This will also dissipate some of the wave's energy. However, most of the energy of the wave would rebound and sweep around the star to the pole of original impact. Additional plasma would be ejected from that pole. At each pole, some of the energy of the wave would be dissipated as plasma is ejected off the pole.
If one single massive wave were to move back and forth over a star, the stars center of mass will shift back and forth.
Second, imagine the second simplest situation, with two massive waves moving in opposite directions. In this example, the two waves pass each other in opposite directions at the "equator" of the star and reach opposite poles at the same time. A pair of such waves might be created by a large object with a quick death spiral impacting into the star.
Graphic of death spiral
As the large object spirals in -- just above the "equator" -- the massive transitory gravitational pull between the two bodies would pull a mountainous ridge of plasma above the star's normal plasma ridge.
Graphic of ridge of plasma
After impact, the gravitational pull of the impacting body would not exist. The ridge of plasma would collapse rushing as two waves in opposite directions.
Graphic of plasma ridge collapsing and flowing around the star
In this scenario, the waves would not be perfectly symmetrical -- at first -- because the forces between the star and impacting object become stronger, and circle the star, as the impacting object spirals inward. But after the waves had swept back and forth over the star a number of times, they would gradually even out and become symmetrical. A significant difference would exist between this scenario and the first: as the waves approach each other at the equator, they would superimpose, and eject some of their material off at the equator. This would create a disk of material ejected from the equator of the star as in the case of Eta Carinae.
Graphic of waves colliding and ejecting equatorial disk material
If two massive waves were to move back and forth over a star, the stars center of mass would remain stationary.
Keep in mind that the energy of the plasma ejected off the star could be much greater than the energy of the impacting object. This might seem odd at first. A natural first thought would be that impacting energy would be greater than the energy carried away by the ejected plasma. However, as an impacting object sets up initial waves over a star, the stars own existing waves would be modified by induction, thus aligning with those created by the impacting object. The impact, if large enough, would define the destiny of the star. The energy that is naturally released by the decaying core of the star could take over, and long after the energy impulse of the initial impact dissipates, the star could keep pumping out plasma into space.
Graphic of harmonic waves before impact versus nonharmonic waves after impact
It is possible that the waves started by the impacting object might create a situation that gradually destabilizes the core. Over time, instead of settling down, the core might release energy that makes the waves stronger. This might destabilize the core even more, releasing even more energy, in a chain reaction-like fashion.
It is possible that a strong impact might make the star go through numerous periodic or semi-periodic novas.
It is also possible that a strong enough impact would break the core -- causing it to go supernova.
What would be the geometry of the plasma ejected by the core? The simplest way to understand how the plasma would be ejected from the core of a star is to analyze how electric and magnetic fields interact over a sphere. Keep in mind the plasma in the outer envelope is ionized, and the inner core of the star has very strong electromagnetic fields on its surface. As the waves sweep over the star either the electric or the magnetic field will dominate. Either the electric or magnetic field will dominate by sweeping from pole to pole.
Graphic of electric field waves dominating
Graphic of magnetic field waves dominating
For this example, I will assume the electric field is sweeping from pole to pole. As this primary field sweeps from pole to pole, it will induce magnetic fields at right angles, parallel to the equator. On one hemisphere, the magnetic fields will rotate in one direction, and on the opposite hemisphere, the magnetic field will rotate in the opposite direction.
graphic
At the poles the intensity of the electric field will dominate, but the magnetic field will still be important. As the ionized plasma is ejected off the core of the star, the massive electromagnetic fields on the surface of the core will shape the ejected plasma by induction. The effect of the fields on ejected plasma will cause the plasma to form into a spherical shell. At first, the plasma starts to form an open-cup shape, but as the plasma starts to turn, it wraps around into a closed shell -- just as Eta Carinae has done!
animation of Eta Carinae lobes expanding
Keep in mind, the electric and magnetic fields in the ejected plasma are not only being affected by those from the parent star. The fields in the ejected plasma interact as well. Part of the reason the plasma creates a spherical shell as it is ejected is because the cross product between the electric and magnetic fields in the ejected plasma creates a focal point of induced gravity. The induced gravitational field helps turn the plasma -- it helps create the spherical lobes that are seen in many planetary nebulae. This is exactly why Eta Carinae's geometry is not a fluke.
graphic
A very interesting detail in the Hubble images of Eta Carinae are the "lines" that appear to pass through the nebulae: some sweeping from pole to pole; and others parallel to the "equators" of the two lobes.
Graphic of lines
These lines exactly match those predicted by the Ball-of-Light Particle Model and are simply caused by localized areas where the electric and magnetic fields are more intense. It is as if the electric and magnetic lines of force were drawn into the nebula. They are exactly like the lines a bar magnetic makes in iron filings in that classic physics demonstration of the magnetic field.
It is interesting to note, in spherical harmonics, the first harmonic has a central sphere with two lobes at opposite poles. The second harmonic has a central sphere, two lobes at opposite ends, and a central disk.
Graphic
If the waves that sweep across the core of the star are strong enough, all of the enveloping plasma would be ejected. This would leave behind the white-hot core -- bare and visible. This bare core would emit non thermal radiation. If completely bare, it could not emit thermal radiation. If the core was able to create a thin envelope -- creating new material faster than the waves could sweep new envelope material off the core -- there might be a small percentage of thermal radiation mixed in with the large percentage of non thermal radiation.
Graphic of star with core and envelope emitting thermal radiation
Graphic of star with waves sweeping off envelope emitting thermal and nonthermal radiation
Graphic of a bare core emitting nonthermal radiation
Such bared stellar cores are found at the centers of planetary nebulae. It is interesting to note, the spectroscopy of some white dwarf stars is known to be nonthermal. Even if it wasn't already known, the Ball-of-Light Particle Model would still predict many white dwarfs would give off nonthermal radiation.
The central star of Eta Carinae is predicted to be a Blue Giant. It may very well turn out to be a White Giant -- a giant version of a white dwarf.
What would be the composition of the material in the nebulae? Part of the material ejected from the star would be made up of normal electrons and protons. However, the unusual intensity of the waves in this situation could easily induce larger atomic nuclei -- such as helium or iron nuclei.
Since a planetary nebula is a fairly violent event, it might be possible for the core of the central star of a planetary nebula to eject elementary particles -- balls-of-light -- that are: meters across, tens of meters across, hundreds of meters across, or possibly even thousands of meters across. Unlike the normal elementary particles like electrons and protons, most of these larger balls-of-light would not be stable. In essence, they would quickly start decaying into smaller particles. An example of this can be seen in the Helix nebula:
graphic
These objects are rapidly decaying balls-of-light. The images were taken by the Hubble Space Telescope and are located in the nebula area of the Helix Nebula. You can not actually see the surface of the balls-of-light in this image. Each of these rapidly decaying balls-of-light has its own "mini" nebula made of ejected material. The central star in the Helix Nebula has a massive nebula caused by the primary decay of the star. Each of these objects is a secondary decay -- with a secondary nebula. While these secondary nebulas are "small" or "miniature" in size compared with the overall nebula, the outer spherical size of these "mini" nebulas is estimated to be about twice the size of our solar system -- several billions of miles across! Again, these are rapidly decaying balls-of-light.
The Hubble Space Telescope has a new infrared camera. An image of these objects will surely show a very hot and dense object at the centers of these mini nebulae.
I recommend that these individual decaying balls-of-light are monitored closely on a regular basis. I would expect they could suddenly become unstable and violently explode.
Not all ejected balls-of-light in a planetary nebula would be this large. Smaller particles tens of meters across might exist for hours to months at a time. While these smaller particles decay, they would emit electromagnetic radiation off their poles -- the wavelength being comparable to the size of the object. They would almost be like mini pulsars. The electric and magnetic fields from these smaller balls-of-light might also align the plasma around themselves creating short-term masers. It is interesting to note: masers have been observed in Eta Carinae's Nebula emitting powerful pulses.
As the massive waves sweep across Eta Carinae's core, they approach the poles. As they approach the poles, their intensity would increase until it peaks when it reaches the pole. The closer the waves get to the poles, the more they should induce short-lived balls-of-light that are relatively unstable and decay rapidly. After the waves change direction at the poles and sweep in the opposite direction, their intensity would suddenly drop off. This would cause the a unique pattern in timing of x-rays coming from Eta Carinae. The x-rays would gradually increase, then rapidly drop off. A team of scientists -- led by Dr. Michael Corcoran of the Universities Space Research Association, Columbia, MD -- has found that,
"X-rays emitted by hot gas near the star initially increased over a period of months and then rapidly diminished in intensity in a matter of days."
Note, the x-rays come from areas within the nebula, they are "emitted by hot gas." This indicates the x-rays must be coming from something recently ejected by the star. Also note, the x-rays come from areas, "near the star." This occurs because the balls-of-light that decay and make these x-rays are inherently unstable and can not travel far from the core before they slow down, become unstable, and decay.
graphic of balls-of-light being ejected and rapidly decaying
To summarize: some of the particles induced and ejected by the core could be small, stable, normal elementary particles; some of the particles induced and ejected by the core could be large, unstable, unusual elementary particles.
See also Helix Nebula
See also HH30.
See also baby stars.
See also "blobs" balls-of-light being ejected from nova the recurrent nova T Pyxidis. This image has more than 2,000 ejected balls-of-light in an area less than 1 light-year across.
See also balls-of-light being ejected from supernova (x-ray balls).
See also balls-of-light being ejected from the sun (x-ray balls, and blinkers).
See also blobs being ejected by "black holes".