Gravitational Induction of an Electromagnetic Wave on a Ball-of-Light

---

Electromagnetic Waves on a Ball-of-Light

Imagine a ball-of-light. On its surface are patches of electromagnetic waves.

Each of the color patches in the above graphic represents an electric or a magnetic field. If the patches are equally sized, and alternate between electric and magnetic over the entire sphere, then the ball-of-light is harmonic. (In other words, this is not a harmonic ball-of-light since the sizes vary.)

These fields -- these patches of electric and magnetic fields -- could be stationary or moving on the sphere's surface.

If the patches of electric and magnetic do not alternate in a symmetrical fashion or are of different sizes, as emphasized in the following graphic, then the ball-of-light is not harmonic.

In cases like this, similar patches of electric or magnetic fields could electrostatically repel each other -- just as two electrons repel each other, or just as the north poles on two different magnets repel each other. The patches could push each other apart. Once moving, the patches can spin around the sphere in various patterns. These patterns might dissipate the energy of the nonharmonic fields, allowing the ball-of-light to settle down and become harmonic. Or, these patterns might accelerate each of the patches of nonharmonic fields: possibly robbing the ball-of-light of energy in the form of photons, possibly causing it to decay rapidly, possibly splitting it into smaller parts, or possibly causing it to explode. (See also, Decay Modes)

Electromagnetic Induction

If one ball-of-light moved past another ball-of-light, then the electric and magnetic fields on the surface of each could induce new fields on each other. In general, this would occur if the two objects passed each other at relatively close distance at relatively high speeds.

(See also, The Artificial Decay of the Lithium Nucleus)

Gravitational Induction

If one ball-of-light moved past another ball-of-light at relatively long distances at relatively low speeds, it is still possible that new electromagnetic fields would be induced on each particle due to gravity. However, it would require the masses of the objects to be relatively large. For example, a star, a planet, or a massive comet orbiting a star could induce such fields on the core of a star.

Gravitational Induction of an Electromagnetic Wave on the Core of a Star

To demonstrate this, I have drawn a graphic of a planet orbiting a star:

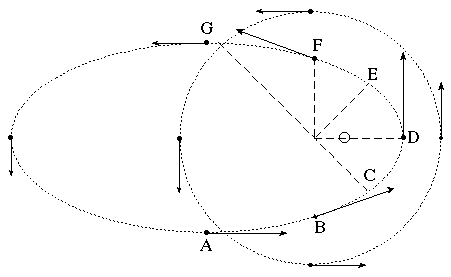
This image has two orbits: one almost circular, one very elliptical. The core of the central star would be relatively unaffected by gravitational variations from the planet in the circular orbit. However, the elliptical orbit could very easily disrupt the core of the star if the planet was massive enough.

Assuming that a massive planet is orbiting the star with an elliptical orbit:

1. At "A" the mass is starting to significantly accelerate, but because the direction is aimed towards the star, the gravitational impact would be small.
2. At "B": the mass is starting to change direction significantly; this would create a gravitational variation that would start to impact the stability of the star's core.
3. At "C": the mass is accelerating forward and sideways; the affect of the gravitational wave on the star's core from this change in the orbiting mass's direction intensifies, further destabilizing the star's core.
4. At this point: the mass has accelerated to its maximum velocity, but its destabilizing affect on the core probably is not at its maximum.
5. At about this point in the orbit the change in the gravitationally induced wave on the star's core reaches its peak. The star will experience maximum instability, and maximum rate of decay.
6. At about this point, while the star is still relatively unstable, the star starts to settle down and become more stable again -- unless, the maximum point of instability at about "E" has already caused the star to go: Planetary, Nova, or Supernova.

The Relative Affect of the Planets on the Sun

In our solar system, each of the planets will have a destabilizing affect on the sun's core as they traverse their orbits. The relevant information for each planet is:

Planet	Mass Relative to Earth	Mean Distance from Sun	Eccentricity	Mean Orbital Velocity	Affect on Sun's Core Relative to Earth
Mercury	0.553	0.3871 AU	0.2056	47.89 km/s	.42
Venus	0.8150	0.7233 AU	0.0068	35.03 km/s	0.28
Earth	1	1 AU	0.0167	29.79 km/s	1
Mars	0.1074	1.5237 AU	0.0934	24.13 km/s	0.74
Jupiter	317.833	5.2033 AU	0.0482	13.06 km/s	2092.83
Saturn	95.159	9.5162 AU	0.0553	9.64 km/s	970.54
Uranus	14.54	19.165 AU	0.0479	6.81 km/s	182.16
Neptune	17.204	30.003 AU	0.0096	5.43 km/s	54.20
Pluto	0.0022	39.503 AU	0.2493	4.74 km/s	0.18

(Note: the numbers in columns 2, 3, 4, and 5 are very accurate. The numbers in the 6th column are an educated guess -- angular momentum of planet times eccentricity -- meant only to give the reader a feel for the topic.)

In the first column is the planet name. In the second column is the mass of the planet relative to earth. In the third column is the mean distance of the planet from the sun in astronomical units -- AUs. More important is the variation of the angular momentum of the planet as it orbits the sun. The sixth column gives a feel for this by simply multiplying the angular momentum of the planet by its eccentricity. (The values were then normalized by dividing by earth's value.) The more eccentric the orbit of the planet, the more the angular momentum varies. For example, Jupiter has the most impact on the sun's core because of its high angular momentum relative to the other smaller planets.

The most dangerous scenario for the sun would be if Jupiter, Saturn, Uranus, and Neptune all reached their perihelion -- their closest approach to the sun -- within months of each other. Jupiter's orbit takes 11.86 years.

Hotter radiation and ultraviolet rays mean more than just needing polarized glasses or sunscreen, but mean very harmful consequences for all life.

Saturn's orbit takes 29.46 years. Uranus's orbit takes 84.02 years. Neptune's orbit takes 164.76 years. The chances of all of the major planets aligning is slim. However, in the history of the solar system, this certainly has happened.

The key detail is, Ball-of-Light Particle Model predicts that the alignment of massive planets in elliptical orbits around a star is dangerous for the stability of the star's core -- or life on the surrounding planets! There just may be a sound scientific reason for the historical "superstition" that apocalyptical events happen when the planets align.

What are the negative impacts of gravitational induction on a star?

The negative affects that a massive planet, comet, or star would have if it was orbiting another star in a very eccentric elliptical orbit would include:

• The star would decay faster -- giving off more heat.
• The star would produce hotter radiation. A star producing more gamma rays, x-rays, and ultraviolet rays would have a negative impact on planets with life.
• The star's core would induce more balls-of-light.
• This would lead to more sunspots.
• More sunspots would lead to more solar mass ejections.
• Ejected balls-of-light could explode by a planet, or on a planet.
• The star's core could become unstable enough to "go planetary" -- i.e., create a planetary nebula. (See also, Planetary Nebula, Eta Carinae)
• The star's core could become unstable enough to "go nova."
• The star's core could become unstable enough to "go supernova."

To summarize, the Ball-of-Light Particle Model predicts Jupiter will have the greatest impact on the sun's solar cycle. It is not a coincidence that the sun's solar cycle is almost equal to Jupiter's orbital period. The small discrepancy between the two must be related to the impact of the other planets.

Varying Gravitational Fields

This is really critical topic! While the Ball-of-Light Particle Model predicts that -- for a given orbiting mass and a given star, a highly elliptical orbit will have a more detrimental affect on the central star than an orbiting mass with a circular orbit -- it also predicts that the gravitational "constant" within a spiral galaxy such as ours is not constant over periods of hundreds of millions of years! Again, the gravitational attraction between the sun and the planets is not constant throughout the solar system's orbit around the galaxy!

There are at least two significant periodic accelerations and decelerations that the solar system undergoes as it orbits within the galaxy:

• The centripetal acceleration the solar system experiences as it orbits the galaxy -- sort of like the forces you would experience on a merry-go-round if the whole merry-go-round was moving in one direction.
• The up-and-down acceleration the solar system experiences as it orbits the galaxy -- sort of like the bobbing up-and-down acceleration that a horse goes through on a merry-go-round.

Varying Centripetal Acceleration and Local Gravity

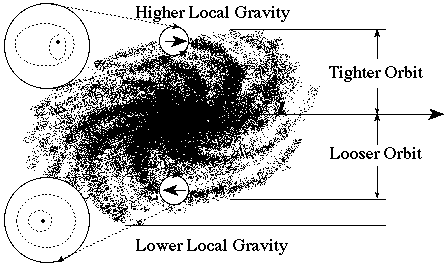
In this graphic, this galaxy is moving to the right. The galaxy is spinning in a clockwise direction. A solar system on the top of the graphic is moving faster than a solar system on the bottom of the graphic due to the simple geometrical relationship of how the angular velocity of the galaxy combines with linear velocity of the galaxy.

As a solar system accelerates around the left side of this galaxy and heads towards the top of this graphic, the local gravitational attraction between the star and its planets increases. As a solar system decelerates around the right side of this galaxy and heads towards the bottom of this graphic, the local gravitational attraction between the star and its planets decreases. As the local gravity increases -- as seen in the top left inset -- the planets' orbits become more elliptical. As the local gravity decreases -- as seen in the lower left inset -- the planet's orbits become more circular.

This is part of the explanation of the mass extinctions that periodically occur on earth roughly every 200 million years.

The Up and Down Bobbing Motion of the Solar System

In this graphic, the dashed horizontal straight line represents the Galactic Plane. The undulating line represents how the Solar System moves up and down -- like horses on a merry-go-round -- as the Solar System orbits the galaxy. At points of maximum velocity, the local gravity will be greater, causing the orbits of the planets to be more elliptical. At points of minimum velocity, the local gravity will be smaller, allowing the orbits to be more circular.

As the earth's orbit varies between being more circular and more elliptical, this cycle will cause long term changes to the earth's climate. This could explain the very interesting phenomenon of the Ice Ages. (An alternate reasonable explanation is the sun rotates around another star in a very long period binary star orbit.) It may also help explain the flipping of the earth's magnetic field's polarity.

To summarize this idea: as our solar system moves through space, its motion speeds up and slows down; speeding up and slowing down changes the gravitational attraction of bodies in the solar system; as gravity's intensity increases in the solar system, the orbiting objects take on more highly elliptical orbits; in general, as gravity's intensity decreases, the planet's orbits become more circular, slower, and wider and this allows the sun to be more stable and decay slower; in general, as gravity's intensity increases, the planet's orbits become more elliptical, faster, and tighter and this causes the sun's core to be less stable and decay faster.

(See also, The earth's 100,000 Year Orbital Cycle)